(wip! needs editing)

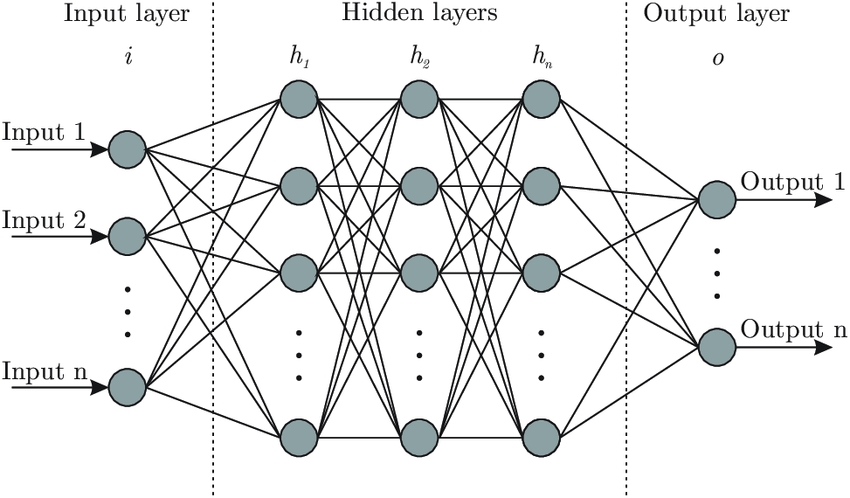
Intro: As sigmoidally-activated neural networks progress through their learning lifecycles, they begin in an untrained phase where weight learning dynamics are nearly a linear dynamical system, but eventually they reach a trained, saturated phase where learning dynamics are nearly static in a system that resembles a graph. After making these concepts formal, a theoretical analysis sheds light on how networks go through these two previously-unspecified/unappreciated training phases. A preliminary result is that juvenile networks approach a clearly-defined intermediate or hybrid phase, where learning dynamics proceed somewhat as if they were a linear dynamical system but also somewhat as if they were a binary decision graph, and that they exit from this intermediate phase to the third phase slower than they arrive from the first phase. A consequence of this analysis is a possible way to conduct initial training that drastically cuts down on the time required to conduct initial training. Also under this analysis, some non-sigmoidal activations such as RELU are identified as having special properties that promote continued learning on more and more data and avoid model saturation suffered by many non-deep machine learning methods.

For context, this project was started when I noticed more or less simultaneously (a) that small weights moving on a straight line are effectively linear, and I've had linear dynamics and eigenvalue solutions to steady-state linear dynamical systems on my mind lately for ESORMA and such; (b) that a network of ones and zeros is a binary graph and can be interpreted as a collection of logical evaluations (e.g. True = A or C or F or G), which also had been on my mind; and (c) that a neural net achieves both seemingly-incompatible scenarios and has to somehow transition from one to the other. I'm presenting the info below in a similar manner of how I came to understand it myself.

Observation 1: If a deep learning vanilla neural network with logistic or tanh nonlinearities (et al*) start with small initial values (as in Glorot for any nontrivial layer sizes), then adjusting weights by small amounts acts in a linear way. That is, the dynamics of learning initially like a linear system even with strongly nonlinear activation functions. (Also includes RELU for values not at zero.) This has to do with the derivatives of sigm and tanh near zero are const (1st derivative) then zero (all higher derivatives). * softmax requires the output values of each part be similar. While logistic on two variables would be y_1=a(W_1x)=1/(1+e^-(W_1x)), y_2=a(W_2x)=1/(1+e^-(W_2x)), softmax instead has y_1=e^(W_1x)/(e^(W_1x)+e^(W_2x)) which is in phase 1 only when W_1x and W_2x are approximately equal (invariant to magnitude or sign) in addition to being within the phase 2 peaks.

Observation 2: When a network is highly learned, continually trying to learn on it with the same dataset will only increase the absolute value of the weights. That is, the values will tend towards +/- infinity. Put through tanh or sigmoid (wlog, let's use sigmoid), then the outputs of layers, ie the y values in y=sigm(Wx), will tend to be just below 1 or just above zero. An operator with values basically at either zero or one is a binary matrix, which can be interpreted as a graph or logical decision process, in the sense that a w.dot(x) gets assigned a 1 or 0, which can be interpreted as a truth value assignment. Even if a multilayer network's input features are not {0,1}- -valued, the output of a saturated (aka fully-learned) first layer will be {0,1}-valued, which upholds the subsequent binary graph interpretations. (Saturation can also be evaluated by how many signs of weight updates flip between training epochs.)

So, several questions arise:

• Am I correct? I.e., does a linear approximation actually work and is an effective approximation, and does the information flow actually look like a binary graph later? And how well does a binary graph or reflect a decision process of any kind?
• A linear approximation would be helpful for providing a single closed-form step to do initial training. What else can the linear approximations do?
• Does the network actually ever achieve binary graph-like activity? What engineering or modeling/explanatory advantages can be gained from understanding the learned network as a simple binary graph 'flow'? Can learned network binary graphs be compressed, via a method like quine-mcclusky or something else?
• Somewhere along training, a network's learning adjustments change from resembling that of a linear dynamical system/process into a binary graph, network flow, or decision flowchart, or logical evaluator. Is there a 'middle zone'? What does it look like, or how long does it last, or how much does it resemble one of the other two models, or does the learning switch in a fell-swoop step, a gradual shift, or something more complex?

To think about:
• A VNN network tends to learn an orthogonal eigenbasis, one component at a time. (Saxe, 2013, Exact, and Andrew & Stephen at PDP. I could use a more concrete source...) Does this relate to learning dynamic linearity?
• What do error or performance curves look like at various stages?
• the funky relationship between, say, the heaviside step function and RELU; the softplus and logistic; erf and normal :: their linearity-logicalities are based on derivatives and these are derivatives of each other, so if we can say something about one's function while knowing about the learning derivatives, we can understand the function better. ie, :: actual computing function and learning dynamic. / consider softplus, y=log(1+e^x). it's second derivative is a logistic distribution-shaped bell curve, meaning it's most nonlinear at x=0, which would be a bad place to start in situations where you want to do linear dynamic styled learning at first. / Also, about RELUs being hybrid logic-linear units: in a sense, they achieve an intermediate between sigma (plain-linear) [dynamics] and pi logical computation. ie they're a rho in a sense... wait are they really actually linear in function as well as in learning dynamic? ... ie when the weights are smaller than the 2nd deriv peaks by plenty, then even somewhat varied input units still get a linear response from sigmoidal activations. It would likely be scaled because of the activation's action, but it's still a fully linear relationship and doesn't qualitatively differ. (ie, if say the weights and inputs numerically cause the logistic activation to yield values all between 0.4 and 0.6, then the linearity measures stay within about [-m/2,m/2] for m=value at peak. Not ideal and it ) / total aside: this function has an amazing 2nd derivative where the linear-to-intermediate transition is 'symmetrical' to the intermediate-to-logic phase. h\left(x\right)=\frac{1}{\left(1+2^{2^{x}+2^{-x}}\right)}
• How RELUs relate. When an activation is zero'ed out by a negative value to the RELU, it's as if it were logically annihilated. But at the same time, when an activation is not zero'ed out, it behaves completely linearly. What effect does this 'hybridization' of binary and linear structure do to the network, and how do we interpret its phases in this context? This also implies we ought to take a closer look at soft-RELUs like Softplus = ln(1+e^x) = integral of sigmoid, gaussian linear error unit = x*Phi(x) = x*(c.d.f of normal distr) = .5x(1+erf(x/sqrt(2))), and LeakyRELUs.
• In a layer with multiple outputs (ie, \ul{y} \in \mathbb{R}^n), each y_i's transition from linear-like to logical-like is independent of any other y_j's. But is there any other interesting dynamics, with regard to either (a) quasi-gradient methods where the change of one weight actually does alter how another weight changes, like maybe Adam but not SGD; or (b) deep layers and how the change gradients of later layers affect changes of shallower/earlier ones?
• A nice bit: the third phase of learning being like a not-fully-connected graph is rather consistent biologically plausible and consistent with what we know about neurons: namely, that they prune their connections to others with age. A side thought: RELUs interpreted as linear/logical hybrids reflect this also: they model *dendrite connnections* which prune connections to other neurons but are still plastic and sensitive to weights whenever they aren't pruned.